kobon triangles in javascript
I wrote this script to generate unique Kobon triangle patterns.
The demo below shows a graphical representation of the program’s output. The code can also be executed without the graphical display, which is nice for running it in the background on node.js.
The complete code is available on my GitHub page.
Each time you click “generate” a (mostly) random pattern is generated and the number of triangles in the pattern is displayed. The pattern is then displayed with SVG with each counted triangle is colored black.
a little background
The most recent research that I can find on Kobon triangles claims that the following table describes the upper bounds on how many triangles can be generated with a variable number of lines:
| k | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| Clément and Bader's upper bound | 1 | 2 | 5 | 7 | 11 | 15 | 21 | 26 | 33 | 39 | 47 | 55 | 65 | 74 | 85 | 95 | 107 | 119 | 133 |
| best known solution | 1 | 2 | 5 | 7 | 11 | 15 | 21 | 25 | 32 | 38 | 47 | 53 | 65 | 72 | 85 | 93 | 104 | 115 | 130 |
source: Wikipedia
As you can see, not all of these proposed upper bounds have been proven by example. For example, there is no known example of 11 lines generating 33 triangles. But by Clément and Bader’s argument, this should be possible.
My goal was to generate Kobon triangle patterns that demonstrate examples of these unproven upper bounds.
I set up a node.js instance to run this code continuosly until an example set of lines is found that creates a number of triangles that matches the proposed upper bounds (or surpasses any bound) for a given number of lines.
Using this code, I successfully found examples of the proposed upper bounds for 3 to 7 lines, and 9 lines:
pre-calculated best values
Notice that the 25 triangles for 10 lines is not the supposed upper bound, but instead matches the best previously discovered number of triangles. I have not found anything better for 10 lines.
Aside from the 25 triangles for 10 lines example, my code produced each of these sets in only a few seconds. However, I let the code run for weeks trying to find examples of the upper bounds for 10 and 11 lines, and have yet to find any actual examples of these suggested bounds.
I also have been unable to generate examples of the best patterns for 8 lines. I suspect the even number of lines might throw off the code I’ve written.
So, the code still needs work, or perhaps the upper bounds are too high. I don’t say that with much confidence, as I know my code could be better.
how it currently works
The process is simple. This all happens in KobonGenerator::kobonLines()
- Generate N-1 lines (see
getXBS()) - Add a line on x-axis
- Calculate all x-axis intersections of N-1 lines generated in step 1
- Calculate all other line intersections
- Find all line “segments” between 2 interesections
- Use the segments to determine where triangles have been created
- Return a count of the triangles
generating N-1 lines
Although the code doesn’t actually add the first line until after N-1 lines are generated, it’s important to realize that our first line will actually be the x-axis. The N-1 lines plus this x-axis line give us N lines.
If we think of the first line as the x-axis, then we can randomly generate new lines that pass through the x-axis and the y-axis.
Consider the following simple line form:
`y = mx + b`
Since our first line is the x-axis, we can create new intersecting lines by randomly generating values for the for `b` and `x` variables in this equation.
We can then solve for `m` by setting `y = 0`
We can do this because `y` is constantly 0 along the x-axis.
The randomly generated `x` value will determine our x-axis intercept of the new random line, and the random `b` value will determine the y-axis intercept of the random line.
In my generator, the `x` values are increasing as lines are generated, and the `b` values alternate between positive and negative values.
The actual `x` values are spaced randomly, between 10 units and the x-spacing parameter units. The `b` values alternate between positive and negative values. The absolute values are random within the b-range parameter.
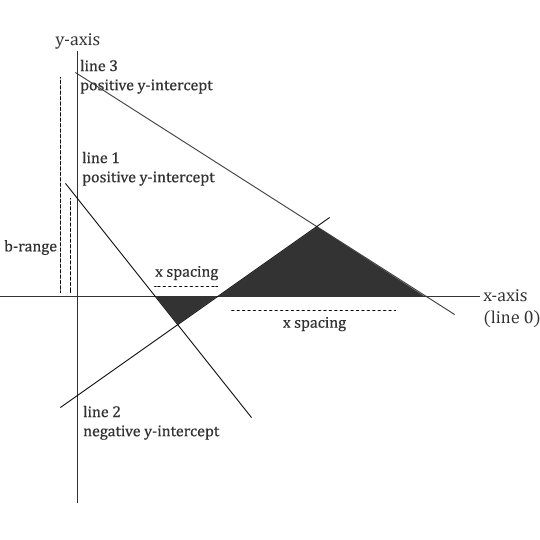
These two limiters on how `x` and `y` intercepts are generated guarantee that as we generate new lines, there will be triangles generated along the x-axis.
I also check to make sure there is good diversity among the calculated `m` values, so lines are not too close to parallel.
Remember that `m` in this equation is the slope of the line. Close to parallel lines would generate stretched out and difficult to see patterns of Kobon triangles.
I decided to make my lines this way after studying some of the line patterns that generate numbers of triangles that are known to be optimal.
line intersections
Once we have all of our lines, all we need to do is solve a bunch of linear systems of equations.
For solving my line intersections, I used gaussian elimination code I found on GitHub, authored by user itsravenous.
My initial hope was to condense all of the line segment intersections into one giant system of linear equations, but this didn’t work out so well.
Each point of intersection is just an intersection of two lines, which means it’s the solution of two linear equations. So, using gaussian elimination is probably over kill, but it’s how I’m finding `N-2` points of intersection for each `N-1` lines.
Note that this is `N^2` complexity. But `N` here is between 3 and 20, so that isn’t too painful. If we start trying to solve Kobon triangles with thousands of lines, we’ll have bigger headaches to deal with.
line segments
The key to finding the triangles lies in the idea of a “segment” of a line. Line segments play a huge role in Clément and Bader’s argument about upper bounds.
A segment is just a part of one of the `N` lines that is sandwiched between to points of intersection. In the previous diagram of 4 lines, we have 6 segments:
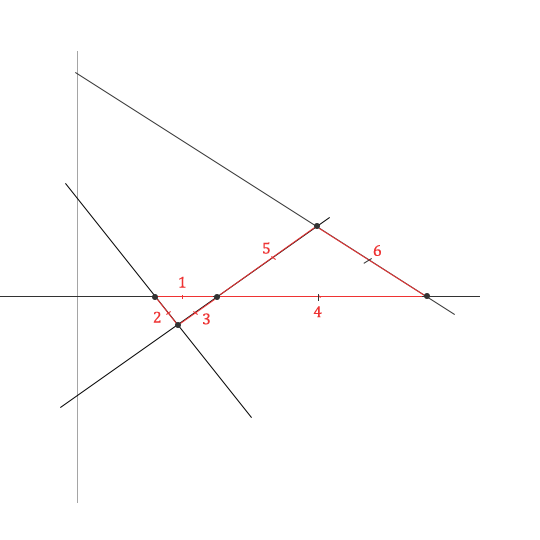
Note that each segment then becomes a part of one of our Kobon triangles. In fact, Clément and Bader argue that in an optimal arrangment of lines, each segment will be a line in exactly one triangle, no more or less.
Clément and Bader’s paper also proposed that in an optimal line pattern, there will never be more than 4 segments touching one point. That is to say that there should never be more than 2 lines intersecting at one point.
With this restriction in mind, I build my data structures for line intersections and line segments as follows:
// line intersection data model
function intersection(line1, line2, point) {
this.line1 = line1;
this.line2 = line2;
this.point = point;
this.segments = [];
}
// line segment data model
function segment(line, intersect1, intersect2) {
this.line = line;
this.intersect1 = intersect1;
this.intersect2 = intersect2;
}
After calculating line intersections, finding segments is trivial. We just sort the intersections on a single line by x-coordinate, and then create segments between each intersection:
// determine line segments between intersections
for (var i = 0; i < lines.length; i++) {
lines[i].intersections.sort(function(a, b){return a.point.x-b.point.x});
for (var j = 0; j < lines[i].intersections.length - 1; j++) {
var seg = new segment(
lines[i],
lines[i].intersections[j],
lines[i].intersections[j+1]
);
lines[i].intersections[j].segments.push(seg);
lines[i].intersections[j+1].segments.push(seg);
lines[i].segments.push(seg);
}
}finding triangles
This is the most confusing part of the code, where we determine kobon triangles from segments
There’s a lot of looping going on here, but the concept is fairly simple.
- We examine each point of intersection.
- Take every pair of 2 segments from the intersection that are part of different lines
-
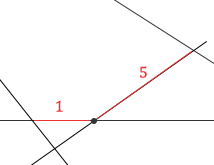
Let’s take segments 1 and 3 for instance:
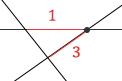
-
Examine the two “other” segment endpoints of segments 1 and 3. Notice that there is another segment that connects these points. It is segment 2.
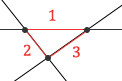
Since we have 2 intersecting segments (namely 1 and 3), and the endpoints of each are endpoints of another separate segment (segment 2), then we just found a triangle!
-
Now let’s take 1 and 5:
-
Do the endpoints of segments 1 and 5 that are not the starting point of examination form another unique segment?
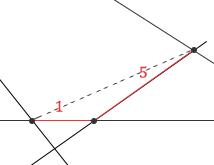
They do not! There is no triangle here…
-
- Repeat until all points of intersection, and all pairs of segments at each intersection, are completely examined.
- Note that we might encounter the same triangle 2 or 3 times. We always check our list of found triangles before adding to it to avoid duplicates.
issues, notes for further work
Obviously there is something not right with my approach. I’m unable to find some previously known best arrangments of kobon triangles for 8 lines, or for any number of lines greater than 10.
I believe the problem is the completely random way in which I find the x spacing and b range values when generating new lines. Although my approach fairs better than a completely random line generation, it does not find all optimal solutions.
I suspect that a more careful approach to adding lines may help the algorithm find actual ideal solutions.
Additionally, I completely exclude the possibility of using one segment for multiple triangles in my counting method. This may be limiting my results.
 trevor simonton
trevor simonton